Introduction
There have been many excellent books and articles that address the difficulties of building a starship. Most approach it from a theoretical perspective and discuss the physics and technical challenges. Rarely do they approach it from a comprehensive engineering point of view. The general conclusion in most of these books and articles is that with current technology it is not possible to build a functioning starship to the nearest stars. In this and succeeding articles I take a different approach and assume we will build a starship in this century using current technology. What would it look like?
Before we can look at the details of building a starship, we need to understand the challenges and put them into context. I wanted to use the SpaceX Falcon 9 “Starship” heavy lifter model for my interstellar starship. Even though the technical challenge of building a starship are an order of magnitude more formidable, to a lesser extent, the same could be said about building a reusable rocket. For fifty years reusability has been an acknowledged requirements for making space accessible for travel, colonization, and resource exploitation. And for fifty years, little progress was made. Tens of billions of dollars had been spent on building and developing the Space Shuttle. The Space Shuttle was reuseable but the labor and difficulties of refurbishing it between launches meant that each flight cost, by some estimates, $500 million. A reusable rocket wound up costing MORE than throwing away a rocket during each launch. The prevailing wisdom was that a privately developed reusable rocket would never occur and that the technology was not yet available to make a reusable rocket that was both cheap and reliable. This was until SpaceX came along early in this century. Within little over 10 years, using a partly reusable first stage, SpaceX succeeded in reducing launch costs by 75% all while developing the most reliable rocket ever built… the Falcon 9. To make this happen, there were no unique technologies that were invented or required. Rather SpaceX built on the knowledge of the prior half century and applied it in new and creative ways.
I believe that part of the reason SpaceX has made so much progress is that instead of using all the reasons why something can’t be done (or only done with vast amounts of dollars) and waiting for the perfect technology, it takes the position that something can be done, done with current technology, and relatively cheaply and quickly. Using this philosophy, my approach was that rather than wait for a better, or perfect technology, approach the challenge with a variation of the expression attributed to Voltaire of “don’t let perfect be the enemy of good”. Using this approach means we can only use technology that either exists or with minor extrapolation, could be available.
The reasons for all the design choices in this and the following articles are greater than can be covered in a few pages so in some cases I will only state the highlights and conclusions. I will review several of the most important conclusions or highlights. Among them:
- To escape the solar system and maximize our velocity, we will need a two-stage configuration.
- 300kps is about the highest velocity we could reasonably attain with current technology. This means that our voyage will be over 4000 years to the nearest stars, or 10,000 years to go to 10LY.
- We will need a nuclear power plant that is both lightweight and high power- able to generate at least 20We/kg of reactor mass.
- It is not possible with current technology to build a starship and dispatch it from our solar system at high speed and have it slow down at the target star. This will drive us to a mission profile whereby most of our reaction mass needed for acceleration, as well as mass required for cosmic ray protection, resupply and deceleration is supplied via enroute packets picked up in the path of our starship. In these articles I will review why this is a requirement as well as some of the engineering and manufacturing challenges of delivering these packets to our starship.
- Our starship will mass about 200,000mt when empty of reaction mass, or 4 million mt during it cruise to the target star.
- A version of a mass driver will be the preferred primary propulsion system both for the starship and for the packets that are delivered to our starship.
This series of articles will cover these highlights.
Problem Scope
The space between stars is vast and current spacecraft travel extremely slow. If the sun were reduced to the size of a typical marble the earth would orbit about 1.4 meters and Neptune about 40m away. On this scale the nearest star would be about 370 km away. The furthest a manned ship has traveled (the moon) is the equivalent of 3mm, though uncrewed automated spacecraft have gone over 150m away over about 50 years of travel.
A starship is a complicated system of payload, power, and propulsion with frequently conflicting requirements. Changing any one aspect will have a cascading effect and force change to other parts of the ship. However, when designing a starship, the overriding challenge is velocity. Velocity is inextricably intertwined with the need for energy. With enough energy (and the ability to control it) these distances are surmountable. Unfortunately, nearly unlimited energy does not exist and to get more energy we have to build larger and larger power supplies that make the mission more and more difficult. Ultimately, we need a tremendous quantity of energy with a small power plant mass.
To more appreciate these challenges, we need to look at a key equation which determines the performance of a rocket- the so-called rocket equation. This equation determines or rockets’ performance.
| EQUATION 0-1: | 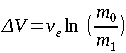 |
Where:
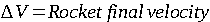

(usually expressed by the term Specific Impulse (Isp) in seconds multiplied by the acceleration of gravity – 9.81mps)
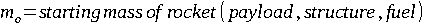

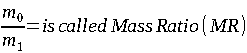
Using the rocket equation, we can determine the performance of a spacecraft knowing only two parameters- the Specific Impulse and the Mass Ratio (MR).
Requirement – the need for High velocity
The Saturn V is to date the largest and most powerful rocket successfully flown. At lift off it weighed about 3000 mt and it had the ability to launch about 140mt into orbit with a velocity of about 7.9kps. If we could place a fully loaded Saturn V in orbit and launched from there, we would have a slightly greater performance since we would not have the drag through the lower atmosphere, gravity losses (the loss of performance from launching vertically) and would have slightly higher Ve because rocket engines have higher performance (specific impulse) when operating in the vacuum of space.
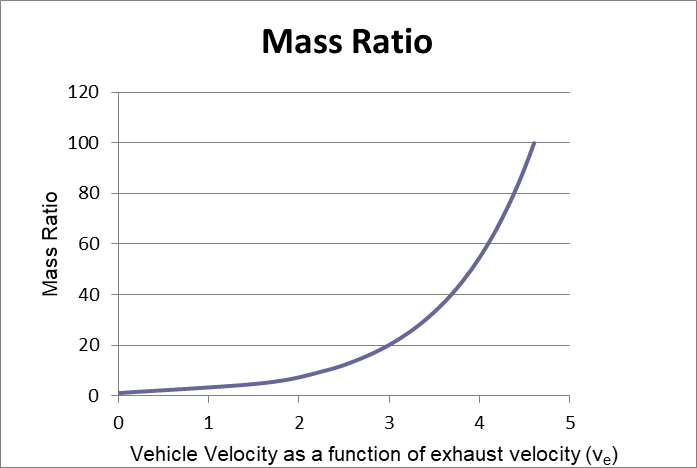
Figure 1. Mass Ration vs Velocity as function of Exhaust Velocity
Would the Saturn V make an effective starship if we launched from space? Using the average performance and mass numbers for a Saturn V, with a final mass of 140mt and running them for the three Stages, we would get a rocket whose final velocity would be about 9.62 kps. While 9.62 is an impressive velocity, it is only .003% the speed of light. It would take over 130,000 years to reach the nearest star. (In reality, it might have difficulty even leaving the solar system since at the earths distance from the sun the escape velocity is about 42kps)
Since MR is a natural log function, greater and greater MR provides less and less increase to your final velocity as shown in figure 0-1. The only other way to get a higher velocity is to increase your specific impulse and have a high exhaust velocity. However, the kinetic energy (KE) equation determines how much energy is in our exhaust velocity. This equation, familiar to high school students everywhere, is:
| EQUATION 0-2: | 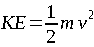 |
This shows us the other half of the problem- our exhaust velocity is the square of the energy given to it. To double our ve, you need to square the energy.
Chemical reactions as used for all current rockets launched from earth are limited by the amount of energy that can be liberated when the fuel is combined with oxidizer. It is true that the temperatures liberated in rocket fuels can melt most metals, but there are usually engineering fixes to these problems. As a rough rule of thumb, specific impulses are directly related to the square root of the exhaust temperature divided by the molecular weight of the exhaust products. The primary limitation for a chemical rocket’s performance is the limited amount of energy (temperature) liberated which ultimately limits their exhaust velocities.
Let’s come up with a hypothetical starship that uses the highest performance chemical rocket typically used – a vacuum optimized engine derived from the Space Shuttle Main Engines (SSME) that burns hydrogen and oxygen. We will assume a specific impulse slightly higher than the original SSME design (460 vs 453) to reflect a larger engine nozzle and higher chamber pressure. Using a single stage with a MR of 20 we would arrive at a final velocity of about 13.5kps.
In the 1950’s and 1960’s Nuclear Thermal rockets were looked at and some prototypes were tested. Nuclear Thermal rockets have been an area of active research and development for 70 years and have demonstrated Specific Impulses in the 850sec plus range. It is believed that improved derivatives of these engines may be able to have a specific impulse of 1,000 seconds, or a little over twice that of the LH/LOX SSME derivative. This would permit final velocities of up to 30kps.
As seen in Figure 0-1, a 20 MR is probably the sweet spot where our final ship velocity is about 3x our exhaust velocity. An MR of 100 will give our final velocity a little less than 5x our exhaust velocity… demonstrating a point of diminishing returns. From an engineering point of view, a 20 MR is difficult if we wanted to launch from earth, since the structure (mainly fuel tanks) would be very large, it would be subject to large aerodynamic forces, and you would have to have massive engines for lift off. However, in space where the gravity and aerodynamic forces are non-existent, an MR of 20 is doable but an MR of 100 is challenging and depending on the fuel which determines the requirements for the fuel tanks, is probably not achievable.
The problem with this analysis is that it does not address the need to stop at our destination. For an interstellar voyage we want to decelerate at our target star/planet which will require the same MR that we needed for our initial acceleration. For our ship that accelerates to three times its exhaust velocity and slows down at the target star we now need a total MR of 400. If we built a ship that massed 10 mt, which including our structure mass (engines, power supply, payload, and empty fuel tanks) our initial staring mass fully fueled, would have to by 400,000 mt. Building a fuel tank to store 390,000 mt of fuel but that weighs less than our 10mt mass available is very difficult and beyond our current capabilities. The only way of reducing our MR is to increase our ve or decrease our starship velocity.
There are propulsion engines that have specific impulses in the thousands and are called electric propulsion- either ion or plasma. They take individual ions and accelerate them with magnetic fields to very high velocity. However, their thrust is very low- frequently a fraction of a newton. This goes back to the fact that tremendous power is required to increase exhaust velocity substantially. Furthermore, electric propulsion is not as efficient as a chemical rocket. Traditional chemical rocket engines are usually over 90% efficient in converting energy into thrust whereas electric propulsion thrusters are typically around 50% efficient in converting electric power to thrust. Furthermore, nuclear reactors or RTG’s convert only a portion of their thermal energy into electrical- in the case of a typical earthbound reactor, about 1/3rd, or in the case of an RTG only about 7%.
For a chemical rocket or electrical propulsion, we can figure out a typical fuel consumption by using the equation:
| EQUATION 0-3: | 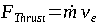 |
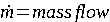
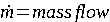
| EQUATION 0-4: | 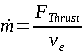 |
The NEXT engine, a successful electric thrust engine used on some current NASA spacecraft puts out about 236mN with a specific impulse of 4200 sec and uses about 7kw. At this thrust and ve the calculated mass flow is about 5.73×10-6 kg/sec. This works out to 1kg of reaction mass used every 2 days. If we used electric propulsion on a starship the size of a Saturn V with a 3000mt m0 and an MR of 20, we would have 2850mt of reaction mass and we would take 15,770 years to expel all this mass! While a high specific impulse is a requirement for a starship, our thrust (and hence mass flow rate) must be hundreds of times higher than typical electric propulsion which would require hundreds of times more power. In theory our 4200 second NEXT engine with a MR of 20 could bump our speeds up to about 123kps. Some electric propulsion engines, with appropriate design modifications and given enough power can have specific impulses of up to 10,000 seconds. If we had an electric propulsion with a specific Impulse of 10,000 seconds, we could achieve a velocity of 300kps and a 4300-year voyage time to the nearest star.
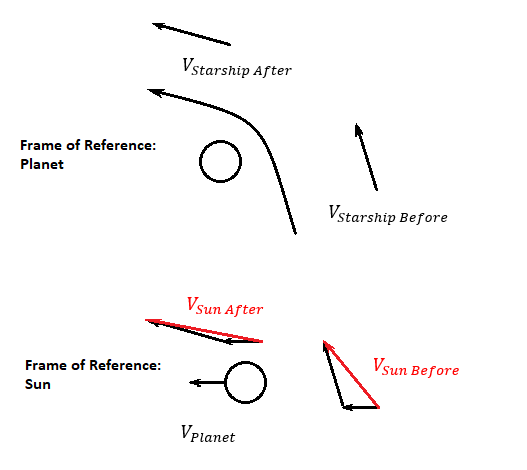
Figure 2. Gravitational Slingshot Planet and Sun Reference
The low force provided by electric propulsion also creates another challenge- escaping the sun’s gravity. Electric propulsion does not have enough power to propel a starship directly to another star- rather they will cause our starship to slowly spiral away from our sun. Depending on the thrust to mass ratio, it can take decades or even centuries to reach solar system escape velocity. During this time the spacecraft will have swung around the sun in a widening spiral without traveling toward its target and wasting a large portion of its fuel.
There are some tricks which may be able to boost our electrically propelled spacecraft velocity- including a Gravitational Slingshot (Figure 0-2) using a planet (usually Jupiter) to boost up the velocity by a few kps. This may be enough to throw us out of the solar system after only a few years of acceleration with electric propulsion. However, this technique can typically add no more than about 10kps and would only work toward boosting velocity in the direction of the planets (in this case Jupiter’s) travel and unfortunately most of our targeted nearby stars are not located there.
Conclusion
The distance between the stars is so vast that even with our best technology, we are talking about voyage times of many thousands of years. This will necessitate a large starship.
The reality of the rocket equation restricts our velocity. A Mass Ratio of about 20 is the sweet spot- it is achievable with current technology and provides a reasonable final velocity- about 3x faster than our rockets’ exhaust. Exhaust velocity is driven primarily by the amount of energy put into our reaction mass- with a chemical reaction this is driven by how hot you get the fuel/oxygen to burn. Chemical rocket engines with an MR of 20 can achieve velocities of only a bit more than 13kps but provide very high thrust and can achieve these velocities in a few minutes. Electric propulsion can provide many times higher velocity for the same reaction mass but require vast amounts of electrical power and provide very low thrust. Typical electric thrusters for a large ship may take many centuries if not thousands of years to expel all their reaction mass and achieve their target velocities.
Using a gravitational slingshot can permit an electric propulsion starship with enough extra velocity to escape the sun but can only add perhaps 10kps to your starship’s velocity.
In the next Article we will address the problem of escaping the Solar System with a two-stage rocket that leverages the high thrust of a chemical or nuclear thermal rocket with an Oberth powered maneuver, and the low thrust but high-performance electric propulsion that can bring our starship up to about 300kps.
For further details, along with expanded discussion of the many challenges that were not addressed or only lightly touched on are available on my website https://www.allthingsspace.info.
About the Author: David W McGuire is a retired veteran from the USAF and AF Reserve where he held various jobs as an Acquisition and Procurement Officer, C-5 Maintenance Officer, Maintenance Squadron Commander and Deputy Group Commander. He retired as a Colonel. He also has worked in the chemical, pipeline and petroleum industries where he held varied positions including Terminal Manager, Regional Accountant Manager, Regional Engineering Manager, and Regional Operations Director. He has a degree in Aerospace Engineering and an MBA.

